技術ブログ

幾何公差は製品設計と製造の世界における中心的な概念です。部品の形状、位置、その他の3次元特性を厳密に制御し、製品の機能性や組み立て易さを大きく左右します。

この記事では、幾何公差に関してわかりやすく解説していきます。記号一覧から種類、測定方法、そしてデータムと寸法公差との微妙な違いに至るまで、幾何公差の全体像を網羅的にご紹介します。

また、JISを含む様々な規格に基づいた、平面度や位置度などの公差の解釈や、技術図面での表現方法についても詳しく掘り下げていきますので、ぜひ、参考にしてください。

幾何公差とは？寸法公差との違いは？

参照：https://kikakurui.com/

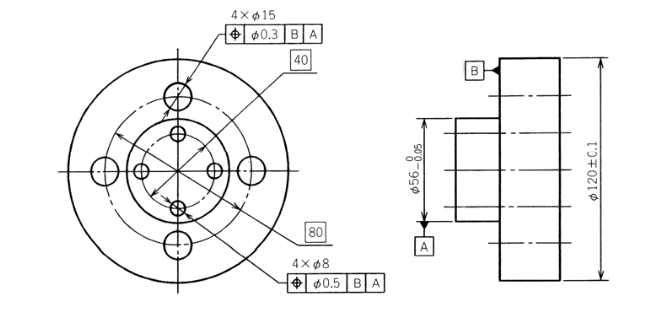
幾何公差とは、製品の形状や特徴の精度を定義するための工学的概念です。製品の形状、姿勢、位置、振れなどの3次元的特性が設計要件を満たしていることを保証するために用いられます。

単に寸法の精度を示す「寸法公差」とは異なり、製品の機能性や組み立ての容易さに直接的な影響を及ぼします。

寸法公差は、製品の特定の線形寸法（例えば長さ、幅、高さ）の許容範囲を示し、JISにおいても同様に定義されています。これに対し、幾何公差は製品の形状や相対的な位置をより厳密に制御し、平面度、直角度、円筒形度などの属性に関する許容範囲を定めます。

製品の品質と機能性において、この差異は非常に重要です。寸法公差が主に製品のサイズの変動を制御するのに対して、幾何公差は製品全体の形状や部品間の相互位置関係を保証するために使用されます。

特に、精密な組み立てや高度な機能が要求される製品では、幾何公差の適用がその性能と信頼性を保証するために不可欠です。

幾何公差の基準「データム」について

幾何公差の基準「データム」とは、製品設計や製造において非常に重要な概念です。

寸法や形状を測定する際の基準点や面を示し、精度の高い製造を保証するために必要不可欠です。

ここからは、データムの役割、そしてその使い方について詳しく解説していきます。

データムとは

幾何公差におけるデータムとは、製品の特定部分を基準点または基準面として設定し、その基準を用いて他の部分の寸法や位置を測定・制御するための基準です。

データムは、製品設計において非常に重要な役割を果たし、幾何公差の測定や評価の出発点となります。データムは、製品の機能や組み立ての要件に基づき、精度が要求される特定の面、線、点などを指します。

例えば、部品を組み立てる際に、特定の面を基準として他の部品を位置づけるためにデータムを使用します。データムは、その他の寸法や特徴がどのように製品全体に関連しているかを明確にすることで、製品の品質と一貫性を保証します。

この基準点や面の選定は、製品の設計段階で慎重に行われ、製造プロセス全体にわたって一貫して遵守される必要があります。

データムの書き方

幾何公差におけるデータムの書き方は、製図規格に準じた明確な方法で行われます。

データムの指示は、通常、製品図面上でデータム記号と関連する幾何公差とともに示されます。データム記号は、一般的に大文字のアルファベット（例えば「A」「B」「C」など）を用いて表され、これらは特定の基準面、線、または点を指します。

図面上でデータム記号は、それが参照する基準要素の近くに配置され、通常は直角三角形の記号内に文字が含まれます。

この記号は、対象の基準要素への矢印やリーダーラインで直接リンクされることが多いです。データムに関連する幾何公差は、データム記号を参照する形で指定され、これによりその公差が基準とする具体的な基準点や面が明確に示されます。

幾何公差の記号一覧と種類

JISなどで用いられている幾何公差の記号、種類を下記一覧にまとめました。

公差の種類	記号	名称	説明
形状公差	—	真直度	直線形体の幾何学的に正しい直線からの狂いの大きさ
	▱	平面度	平面形体の幾何学的に正しい平面からの狂いの大きさ
	○	真円度	円形形体の幾何学的に正しい円からの狂いの大きさ
		円筒度	円筒形体の幾何学的に正しい円筒からの狂いの大きさ
	⌒	線の輪郭度	理論的に正確な寸法によって定められた 幾何学的に正しい輪郭からの 線の輪郭の狂いの大きさ
	⌓	面の輪郭度	理論的に正確な寸法によって定められた 幾何学的に正しい輪郭からの 面の輪郭の大きさ
姿勢公差	//	平行度	データム直線、データム平面に対して平行な幾何学的直線または 幾何学的平面からの平行であるべき直線形体又は平面形体の狂いの大きさ
	⊥	直角度	データム直線、データム平面に対して直角な幾何学的直線または 幾何学的平面からの直角であるべき直線形体又は平面形体の狂いの大きさ
	∠	傾斜度	データム直線またはデータム平面に対して理論的に正確な角度をもつ 幾何学的直線または幾何学的平面からの理論的に正確な角度を 持つべき直線形体及び平面形体の狂いの大きさ
位置公差	⊕	位置度	データム直線または他の形体に関連して定められた理論的に 正確な位置からの点、直線形体または平面形体の狂いの大きさ
	◎	同心度	データム円中心と同一中心上にあるべき点のデータム円中心からの狂いの大きさ
	◎	同軸度	データム直線と同一線上にあるべき軸線のデータム軸直線からの狂いの大きさ
	⌯	対称度	データム軸直線又はデータム中心平面に関して互いに対称であるべき形体の 対称位置からの狂いの大きさ
振れ公差	↗	円周振れ	データム軸直線を軸とする回転面を持つべき対象物又はデータム軸直線 に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに 回転したとき、その表面が指定した位置又は任意の位置で 指定した方向に変位する大きさ
		全振れ	データム軸直線を軸とする回転面をもつべき対象物又はデータム軸直線 に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転した その表面が指定した位置又は任意の位置で指定した方向に変位する大きさ

参照：https://kikakurui.com/

幾何公差の種類について詳細を解説していきます。

形状公差

形状公差は幾何公差の一種で、製品や部品の形状が基本的な幾何学的な理想形からどの程度逸脱しているかを示します。

製品の平面度、直線度、円度（丸み）、円筒形度など、特定の形状特性の精度を制御するために用いられます。例えば、平面度の公差は、製品の面がどれだけ平坦であるかを定義し、直線度は線がどれだけ真直ぐであるかを示します。

形状公差の適用は、製品の機能に直接影響する可能性があるため、特に精密な製造が必要な分野で重要視されます。例えば、エンジン部品や高精度な機械装置では、部品間の正確な適合や滑らかな動作のために、形状公差が厳密に規定されています。

形状公差を適切に指定することで、製品の品質を確保し、製造プロセス中の不具合を最小限に抑えることが可能です。

姿勢公差

姿勢公差は幾何公差の中で、製品や部品の特定の面や軸の向きや角度の精度を定義するために使用されます。平行度、垂直度、傾斜度などが含まれ、製品の特定の要素が他の要素や基準とどのように位置関係を持つべきかを規定します。

たとえば、平行度の公差は二つの面が互いにどれだけ平行である必要があるかを示し、垂直度は一つの面が基準となる面に対して完全に垂直である度合いを定めます。

姿勢公差は、部品の正確な組み立てや適切な機能の確保に不可欠です。例えば、ギアやベアリングなどの機械部品では、軸が正確に整列していないと、運動効率が低下したり、過剰な摩耗やノイズが発生する可能性があります。

位置公差

位置公差とは、部品や製品の特定の特徴（穴、ピン、その他の組み合わせ特徴）が指定された基準点や基準軸からどの程度偏っても良いかを定義する幾何公差の一種です。

位置公差は、特に穴やピンなどの部品が他の部品と正確に合わせて組み立てられる必要がある場合に重要です。これは、製品が正しく機能するために、特定の部品の正確な位置合わせが必要な状況で用いられます。

位置公差は、製品の組み立てや相互作用において精密な位置決めが求められる場合に特に重要です。たとえば、エンジンの部品や精密機器では、部品間の微細なズレが全体の性能に大きな影響を与える可能性があります。

位置公差を設定することにより、製品の各部品が設計通りに正確に配置され、製品全体の機能と性能を保証することができます。

位置公差は、製品設計図において、特定の公差ゾーン内で部品の位置がどの程度変動しても良いかを示すために使用されます。これにより、製造プロセスにおける小さな誤差が許容され、製品の組み立てと機能に必要な柔軟性が確保されます。

振れ公差

振れ公差は、幾何公差の一種で、回転体部品の円運動における偏差を制御するために用いられます。軸や円筒形部品が回転する際の中心線や表面の真円度を保証するもので、部品が回転するときに生じる最大許容変動量を指定します。

特にモーターのシャフト、ギア、ホイールなど、回転する機能を持つ部品において重要です。

精密な回転運動が要求される機械装置において、振れ公差が適切に管理されていないと、過剰な振動や摩耗、騒音の原因となり、最終的には装置の性能劣化や故障につながります。

振れ公差は、製品設計図において、特定の部品の回転軸に対する表面の偏差の最大限度を示すために用いられます。この公差の設定により、製造プロセス中の小さな誤差が許容され、同時に製品の信頼性と機能性を維持することができます。

NMR(最大実体公差方式)とLMR(最小実体公差方式)

幾何公差における「NMR（最大実体公差方式）」と「LMR（最小実体公差方式）」は、部品の幾何学的な特徴が許容される公差範囲内でどのように変動するかを定義する方法です。

NMR＝最大実体公差方式では、公差範囲が最も大きな実体（部品）が要求仕様を満たすことを保証します。この方式は、実際の部品サイズが公差の上限に近い場合に、その部品が機能的要求を満たすことを示します。

一方、LMR＝最小実体公差方式では、公差範囲が最も小さな実体が要求仕様を満たすことを保証します。これは、実際の部品サイズが公差の下限に近い場合に適用され、その部品が機能的要求を満たすことを示します。

NMRとLMRの適用により、製品設計者は、製品や部品が許容される公差範囲内で最も極端な条件下でも適切に機能することを確保できます。

幾何公差の測定方法

幾何公差の測定は、製品の寸法や形状が設計仕様内にあることを確認するための重要なプロセスです。専門的な測定機器と技術が必要で、使用される機器にはコーディネート測定機（CMM）、光学測定機器、レーザースキャナーなどがあります。

測定プロセスでは、まず製品の特定の幾何学的特徴を標的として選択し、次に適切な測定機器を使用してこれらの特徴の寸法や形状を測定します。測定結果は、設計仕様と比較され、製品が設計要求を満たしているかどうかを判断します。

正確な測定によって、製品が予定通りの機能を果たし、設計通りの性能を発揮することが確保されます。

公差指示を複数行ってはいけない？

結論、過剰な公差指示は、製造コストの増大や不必要な複雑さをもたらすことがあるため、最小限に抑えることが望ましいです。

重要なのは、複数の公差が部品の機能や製造可能性に矛盾しないことです。例えば、同じ特徴に対して形状公差と位置公差を同時に指定する場合、これらの公差が互いに干渉せず、実際の製造工程で実現可能であることが求められます。

複数の公差を指定する際には、各公差が部品の機能的要件をどのようにサポートするかを明確に理解し、設計の意図に合致していることを確認する必要があります。

また、複数の公差を指示する場合、それらが互いにどのように影響を及ぼすかを評価し、必要に応じて優先順位を設定することが重要です。製造過程での誤解や誤った解釈を避け、製品の品質と一貫性を保証することができます。

金属加工についてのご相談は当社まで！

金属加工の世界では、精度、信頼性、そして豊富な実績が業界をリードする要素です。当社は、長年にわたる経験と深い専門知識を持っています。

豊富な経験を持つ技術者が、お客様の要望に全力で応えます。小規模な試作品から大規模な製造ラインまで、幅広いニーズに対応可能です。

まずはお問い合わせフォームから、お気軽にご相談ください！